Since 1973, a new type of controller, the Fuzzy Controller (FC), has emerged. A large number of experiments and experimental results show that this controller controls objects with high nonlinearity, severe cross-coupling, no explicit mathematical model, large environmental disturbances, large control delay, and time-varying characteristics. The effect is better than the direct digital controller. However, the simple application of this controller also has some drawbacks: (1) it causes steady-state errors in the system; (2) the system often has small-scale oscillations within the steady-state range, especially if the object has a purely delayed system. The actuator oscillates continuously in the system; (3) The step input best response parameter of the controller and its best anti-jamming parameter (here refers to the three FC quantification factors, namely the error quantification factor, the error rate quantification factor, the ratio Quantification factors are often inconsistent. These defects seriously affect the optimal control effect of this type of controller, and also indicate that the fuzzy mathematics theory is flawed, that is to say there is an imperfection in FC design methods.
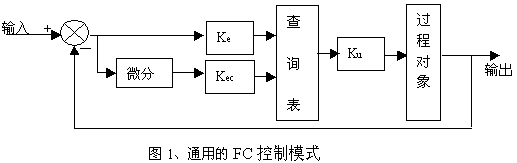
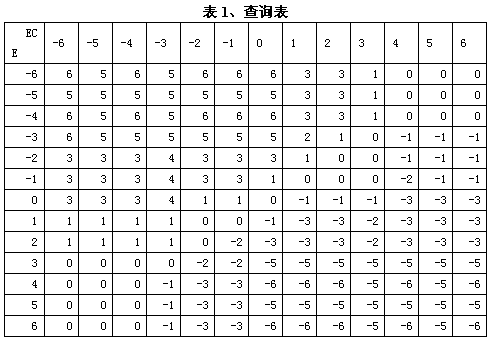
With regard to this theory, pioneers at home and abroad have already done a lot of work. To this day, a relatively complete and practical general-purpose FC control model has been established (see Figure 1). The core is to obtain a query. Table (as shown in Table 1). However, with regard to the essential characteristics of such controllers, from a theoretical point of view, there is still a lack of systematic analysis (data 1), so that in order to improve the control effect of such controllers, people spend a lot of time and money to do experimental exploration work. The purpose of this paper is to discuss these issues theoretically.
One, FC design method flaws
As we all know, the design of general fuzzy controllers is divided into three steps (see documents 2 and 3): First, the amount of fuzzification; the second is the fuzzy operation based on the control rules; the third is the accuracy of the fuzzy quantity. - Fuzzy judgment of output information. The first step is divided into three small steps: 1) The quantitative problem, that is, through a conversion formula, the error and its rate of change are all converted to the range of [-6, +6]; 2) Discretization, that is, the interval [-6, +6] is divided into several blocks; 3) Fuzzification. The third step is also divided into two small steps: 1) refinement; 2) the inverse quantization problem, which means that the refined discrete quantity is multiplied by a suitable coefficient to be converted into the output of the controller. People can pre-complete the above steps 1) 2), 3), 2nd step and 1st step of the 3rd step. The result of this is to get a control summary table, which is the above-mentioned query table (table 1). This control list becomes the core of the fuzzy controller. Everything that people do about fuzzy controllers is centered around this core. However, we can see from the above analysis that FC has a serious flaw in the design method, that is, for the convenience of mathematics processing, the continuous error and its rate of change are discretized, and the final control volume is also a For the sake of convenience on the computer, the discrete work, the design work is over here and there is no final continuous processing of this discrete control amount. Here we should see that it is exactly this discretization of output control that masks the essence of FC and leads to a series of defects that currently appear in fuzzy controllers.
2, FC algorithm formula
2.1 Two-dimensional Universal Algorithm Formula for FC
Our following work is to complement the FC design method imperfections: the discretized FC output is processed continuously. After a careful study of Table 1, through the "fitting" method, after a large number of repeated calculations, and finally summed up, we finally get a FC two-dimensional general algorithm formula:
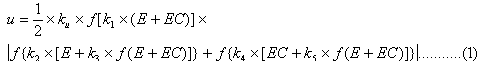
among them
e----error (=set value-feedback);
Ec----error rate change rate;
Ke, kec, and ku are three quantification factors, respectively. Here we need to explain one point: As mentioned in our preface, there are some data that can be used to optimize the parameters of these three quantification factors, like the PID algorithm, which can be used to optimize the proportional, integral, and derivative constants. same. Here we provide
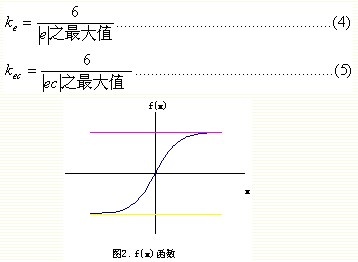
Ki (i=1, 2, 3, 4, 5) - constant coefficient
f(x) is a function of the type shown in FIG. Common hyperbolic tangent functions and arc tangent functions and so on. We will not discuss this function in this paper.
2.2 The physical meaning of the coefficients in formula (1)
For convenience of discussion, the function f(x) in formula (1) is taken as a hyperbolic tangent function, that is,
Therefore, formula (1) becomes
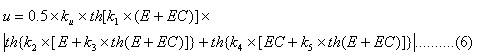
2.2.1 When
(E+EC)
When approaching the maximum, in order for the FC to be able to make adjustments in time, it must be required
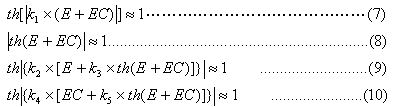
In this way, formula (6) can be simplified as
In the previous discussion, we know that ku is a quantization factor. From the above equation, we know that ku is also the maximum limit value of the FC output (ku>0).
It can be known from formula (7)
K1(E+EC)
>1.5(th(1.5) = 0.905148), ie k1>1.5/
E+EC
Max, when
E+EC
When max=12, k1>0.125. In general, k1 is a convergence factor less than 1, and its size reflects the sensitivity of FC to E or EC. Excessive k1 will make the system too sensitive to error and its rate of change, causing FC overshoot, even The system oscillation is unstable; too small k1 will make the system error and its rate of change sluggish, slow adjustment.
At present, many literatures describe that the fuzzy control system can easily cause oscillation in a small range near the operating point. Herein, this paper considers that there are two aspects: First, the discrete structure of the look-up table leads to the non-linearity of the deadband of the FC; The second is that k1 is too large. Once the lookup table is fixed, k1 is fixed and cannot be modified.
2.2.2 When
K1(E+EC)
When >2.5, Formula (6) can be simplified as
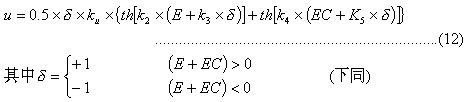
Further partial derivatives of the above formula are available

When E=δ×k3, Formula (13) has an extremum
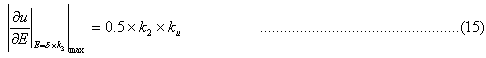
According to formula (15), the size of k2 determines the sensitivity of the FC output to the error, and k3 determines the position of this extreme value (the most sensitive value) on the E-axis, that is, when the system has enough For large errors, the size of k2 and k3 determines the degree of FC response.
When EC=-δ×k5, Formula (14) has an extreme value

According to formula (16), the size of k4 determines the sensitivity of the FC output to the rate of error change, and k5 determines the position of this extreme value (the most sensitive value) on the EC axis, that is, when the system When the error rate of change is large enough, the magnitude of k4 and k5 determines the degree of FC response.
Generally for a closed-loop regulation system, when the set value is abrupt, the error first reaches the maximum value, and then the error rate change reaches the maximum value. In the case of interference to the regulation system, generally, the error change rate first reaches the maximum value. The error then reaches the maximum value, so according to the above conclusions, it can be seen that the size of k2 and k3 has a greater relationship with the adjustment effect of FC when the system setting value changes abruptly. When the setting value is stepped, the adjustment of FC is performed. When ineffective or slowly changing, k2 can be appropriately increased or k3 can be reduced; the size of k4 and k5 has a greater relationship with the adjustment effect of FC when the system is disturbed. In the case of other disturbances, when the FC is not adjusted properly or When the error increases rapidly, k4 can be increased or k5 can be reduced appropriately.
2.3 Verification of the formula
When k1=0.5, k2=0.7, k3=-2/3, k4=0.7, k5=2, formula (6) becomes
When ku=-6 is further taken and E and EC respectively take integers in the range of [-6, 6], a table as shown below will be obtained after calculation.
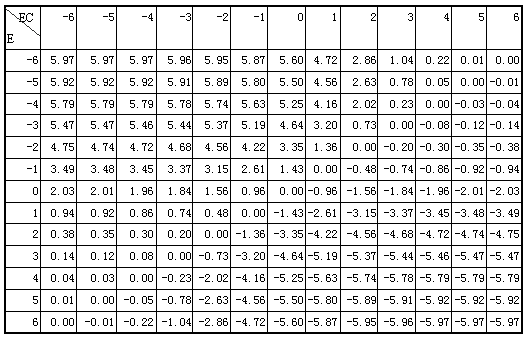
Comparing this table with the previous query table 1, we can see that Table 1 and Table 2 are very similar. This shows that formula (17) summarizes all the information provided by the lookup table 1, or that formula (17) is the result of the continuous processing of the previous lookup table 1.
Third, the simulation results
A simulation comparison experiment was performed on the XDPS-400 distributed control system of Shanghai Xinhua Control Engineering Co., Ltd.
When using a PID regulator, the parameters are as follows: Kp=0.6; Ti=64; Td=0.
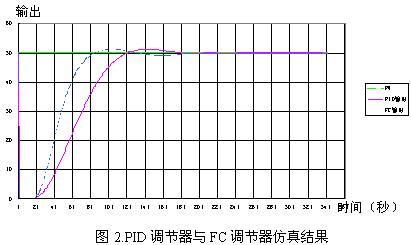
The simulation result under the step response: overshoot = 2.56%, adjustment time into ± 5% error band = 105 seconds.
When FC regulator (output with integral) is used, the f(x) function adopts an arc tangent function. The parameters are as follows: ku=27.6, k1=0.046, k2=0.716, k3=-0.67, k4=0.6, k5=2 , the integral constant Ti = 35.
The simulation result under step response: overshoot = 2.54%, adjustment time to enter ± 5% error band = 75 seconds, as shown in Figure 2.
IV. Corollary - n-dimensional general algorithm formula
In essence, FC is based on the experience of artificial control. For a two-dimensional structure of FC, it mainly controls the process objects according to the magnitude of the extreme rate of deviation. From the theoretical point of view, this is Loss of a lot of information, thus affecting the control effect of this type of controller, especially the adjustment of some disturbances, which makes it very necessary to create a multi-dimensional fuzzy controller nFC. As we all know, according to the traditional method, when the two-dimensional structure of the control table is established, the mathematical treatment is already troublesome enough, and the control core for building a similar control table with a two-dimensional or more structure. Whether people can propose two-dimensional or more control rules is still a problem, not to mention that the mathematical treatment will be very troublesome. The huge amount of calculations makes the design of the two-dimensional or more structural FC almost impossible. However, the previous work in this paper opens up a shortcut for us to create n-dimensional fuzzy controller nFC. We take a careful look at formula (1), which is very regular: f[k1(E+EC)] is a convergence term, and the two terms in the absolute value sign represent the contribution of E and EC to the control action. In this way, we can easily obtain the general algorithm formula of an n-dimensional fuzzy controller nFC.
among them
E(i) or E(j) (i or j=0, 1, 2, ....n-1) -------- are quantified in a certain interval (eg: [-6, 6] Errors and their respective derivatives in ]);
Ks-----convergence factor;
Kj, kj+1 (j = 0, 1, 2, .... n-1) ------ constant, the size of the two together determine the degree of E (j) response to FC;
Ku-----maximum output of the controller;
The definition of the f(x) function is the same as equation (1).
V. Conclusion
In this paper, the general algorithm formula of two-dimensional fuzzy controller is firstly derived from the fuzzy theory, and the formula is discussed in detail. Finally, the simulation and comparison experiment is carried out on the XDPS-400 distributed control system of Xinhua Control Engineering Co., Ltd. The effect is very satisfactory. On this basis, a general algorithm formula for an n-dimensional fuzzy controller is deduced. The formulation of the algorithm has theoretical guidance on the fuzzy control in the control of large inertia, pure lag and other objects as well as in the decoupling control. In addition, the fuzzy controller's method of perfection in the design method proposed in this paper has certain reference effects on the application of fuzzy mathematics in other aspects.
The comany specializes in design and manufacturing the packaging of cosmetics, household cleaning and personal care products. We always focus on the new technology, resin and design and keep launching patented items to meet middle-rang and high-end markets.
Replaceable, reusable, refillable packaging are our mainly development direction, PCR resin, environmentally friendly and pollution-free are our characteristic products.
Airless Bottle,Sunscreen bottle,Nail Polish Bottles,Perfume Bottles,Cosmetic Tube
NINGBO LUX PACK CO.,LTD , https://www.nblux-pack.com